入力データを作成して、学習させる

早速、訓練データとテストデータを作成してみたいと思います。非常に簡単な例として、一次関数のグラフを書いて、適当に点をプロットして、そのグラフよりも下にある点を+1、そのグラフよりも上にある点を-1としたものをデータとして与えることを考えます。適当にPerlでプログラムを書いてみました。

use strict;

if($#ARGV!=3){
  print "invalid parameter.\n";
  exit(1);
}

my $x = shift;
my $y = shift;
my $grad = shift;
my $dataCount = shift;

for(my $i=0;$i<$dataCount;++$i){
  my $x = int(rand($x*100))/100;
  my $y = int(rand($y*100))/100;
  if($x*$grad>$y){
    print "+1 1:$x 2:$y\n";
  } else {
    print "-1 1:$x 2:$y\n";
  }
}

use strict;

if($#ARGV!=3){

print "invalid parameter.\n";

exit(1);

}

my $x = shift;

my $y = shift;

my $grad = shift;

my $dataCount = shift;

for(my $i=0;$i<$dataCount;++$i){

my $x = int(rand($x*100))/100;

my $y = int(rand($y*100))/100;

if($x*$grad>$y){

print "+1 1:$x 2:$y\n";

} else {

print "-1 1:$x 2:$y\n";

}

第一引数がxの範囲(0<x<与えた値)、第二引数がxの範囲(0<y<与えた値)、第三引数がグラフの傾き、第四引数が出力データ数です(あまり細かいチェックはしていません…)。このプログラムを実行すると、次の出力が得られます。

$ perl createdata.pl 10 50 5 10
-1 1:1.24 2:11.13
-1 1:3.83 2:47.31
+1 1:7.34 2:31.71
-1 1:1.73 2:49.64
+1 1:5.65 2:12.46
-1 1:0.16 2:6.02
+1 1:7.67 2:6.43
-1 1:3.54 2:31.12
+1 1:8.64 2:23.84
-1 1:0.75 2:45.21

$ perl createdata.pl 10 50 5 10

-1 1:1.24 2:11.13

-1 1:3.83 2:47.31

+1 1:7.34 2:31.71

-1 1:1.73 2:49.64

+1 1:5.65 2:12.46

-1 1:0.16 2:6.02

+1 1:7.67 2:6.43

-1 1:3.54 2:31.12

+1 1:8.64 2:23.84

-1 1:0.75 2:45.21

とりあえず、一次関数の傾きが1のものと5のもののデータを、訓練用とテスト用それぞれ100データ生成し、訓練用のデータを学習させ、識別までさせてみようと思います。

イメージとしては、次のような感じです。

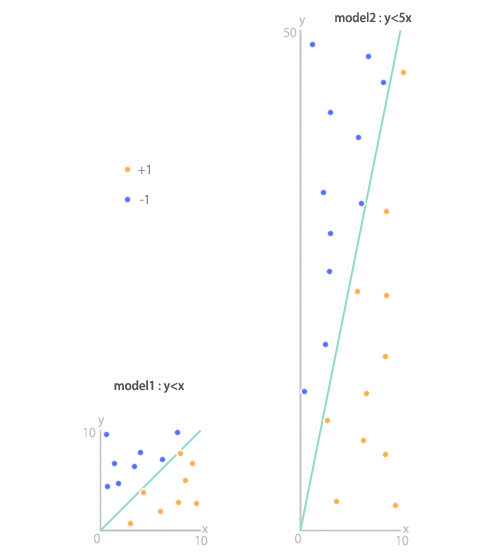
150119

まずは、傾きが1のもの。

$ perl createdata.pl 10 10 1 100
-1 1:4.55 2:8.41
-1 1:6.2 2:9.37
..........
+1 1:6.55 2:6.36

$ perl createdata.pl 10 10 1 100 > learn_1
$ perl createdata.pl 10 10 1 100 > test_1
$ svm_learn learn_1 model_1
TinySVM - tiny SVM package
Copyright (C) 2000-2002 Taku Kudo, All rights reserved.

   100 examples, cache size: 100
..........
Checking optimality of inactive variables  re-activated: 0

Done! 503 iterations

Number of SVs (BSVs)            12 (9)
Empirical Risk:                 0.01 (1/100)
L1 Loss:                        3.77774
Object value:                   -7.71139
CPU Time:                       00:00:00

$ svm_classify test_1 model_1
Accuracy:   96.00000% (96/100)
Precision:  97.91667% (47/48)
Recall:     94.00000% (47/50)
System/Answer p/p p/n n/p n/n: 47 1 3 49

$ perl createdata.pl 10 10 1 100

-1 1:4.55 2:8.41

-1 1:6.2 2:9.37

..........

+1 1:6.55 2:6.36

$ perl createdata.pl 10 10 1 100 > learn_1

$ perl createdata.pl 10 10 1 100 > test_1

$ svm_learn learn_1 model_1

TinySVM - tiny SVM package

100 examples, cache size: 100

..........

Checking optimality of inactive variables re-activated: 0

Done! 503 iterations

Number of SVs (BSVs) 12 (9)

Empirical Risk: 0.01 (1/100)

L1 Loss: 3.77774

Object value: -7.71139

CPU Time: 00:00:00

$ svm_classify test_1 model_1

Accuracy: 96.00000% (96/100)

Precision: 97.91667% (47/48)

Recall: 94.00000% (47/50)

System/Answer p/p p/n n/p n/n: 47 1 3 49

次に、傾きが5のもの。

$ perl createdata.pl 10 50 5 100 > learn_5
$ perl createdata.pl 10 50 5 100 > test_5
$ svm_learn learn_5 model_5
TinySVM - tiny SVM package
Copyright (C) 2000-2002 Taku Kudo, All rights reserved.

   100 examples, cache size: 100
....................   1000     51   100 1.0859  99.4%  99.3%
....................   2000     29   100 0.4554  99.9%  99.6%
.............
Checking optimality of inactive variables  re-activated: 0

Done! 2686 iterations

Number of SVs (BSVs)            9 (7)
Empirical Risk:                 0.01 (1/100)
L1 Loss:                        3.57359
Object value:                   -5.78679
CPU Time:                       00:00:00
$ svm_classify test_5 model_5
Accuracy:   98.00000% (98/100)
Precision:  96.00000% (48/50)
Recall:     100.00000% (48/48)
System/Answer p/p p/n n/p n/n: 48 2 0 50

$ perl createdata.pl 10 50 5 100 > learn_5

$ perl createdata.pl 10 50 5 100 > test_5

$ svm_learn learn_5 model_5

TinySVM - tiny SVM package

100 examples, cache size: 100

.................... 1000 51 100 1.0859 99.4% 99.3%

.................... 2000 29 100 0.4554 99.9% 99.6%

.............

Checking optimality of inactive variables re-activated: 0

Done! 2686 iterations

Number of SVs (BSVs) 9 (7)

Empirical Risk: 0.01 (1/100)

L1 Loss: 3.57359

Object value: -5.78679

CPU Time: 00:00:00

$ svm_classify test_5 model_5

Accuracy: 98.00000% (98/100)

Precision: 96.00000% (48/50)

Recall: 100.00000% (48/48)

System/Answer p/p p/n n/p n/n: 48 2 0 50

両方共、PrecisionもRecallも高い数値が出ています。狙いどおりの結果になったと思います。

これより先の文章は(これまでにも増して)、さらにいい加減なものですが…

これを、仮に、モデルを入れ替えて識別させてみるとどうでしょう。つまり、y<xのモデルにy<5xのデータを与えてみた場合と、y<5xのモデルにy<xのモデルを与えてみた場合の出力を試しに見てみようと思います。

$ svm_classify test_5 model_1
Accuracy:   62.00000% (62/100)
Precision:  100.00000% (10/10)
Recall:     20.83333% (10/48)
System/Answer p/p p/n n/p n/n: 10 0 38 52

$ svm_classify test_1 model_5
Accuracy:   52.00000% (52/100)
Precision:  51.02041% (50/98)
Recall:     100.00000% (50/50)
System/Answer p/p p/n n/p n/n: 50 48 0 2

$ svm_classify test_5 model_1

Accuracy: 62.00000% (62/100)

Precision: 100.00000% (10/10)

Recall: 20.83333% (10/48)

System/Answer p/p p/n n/p n/n: 10 0 38 52

$ svm_classify test_1 model_5

Accuracy: 52.00000% (52/100)

Precision: 51.02041% (50/98)

Recall: 100.00000% (50/50)

System/Answer p/p p/n n/p n/n: 50 48 0 2

上のほうが、y<5xのデータに対して、y<xのモデルで識別した場合です。Precisionが100%ですね。逆にy<xのデータに対してy<5xのモデルで識別した場合はRecallが100%となっています。考えてみればなんとなく分かることですが、学習によって推定された境界線と、実際にテストとして与えたデータを重ねてみると、上記の結果になることは視覚的に分かると思います…、が、多分間違った使い方のような気もしています。

とはいえ、とりあえず、実際にデータを作成して訓練と識別を実際にしてみることで、SVMの使い方が具体的になったと思います。

次は、もう少しSVMが中でしている計算などを追ってみたいのですが、少し勉強のため日が開くと思います…。